复杂的翼弦区

您可以使用复杂的翼弦区在叶片的叶背或叶盆上定义任意的复杂公差带。区域始终从前缘测尖延伸到后缘测尖。中心概念是“复杂区域”，它基于前缘或后缘。

定义复杂的翼弦区

要定义复杂的翼弦区，请执行以下步骤：

1. 将复杂的翼弦区参数添加到“公差”文件中计算选项卡上的选定的计算和参数列表列表中。您最多可以定义10个区域（COMPLEX_CHORD_ZONE到COMPLEX_CHORD_ZONE10）。

2. 使用以下方法之一来设置区域的参数：

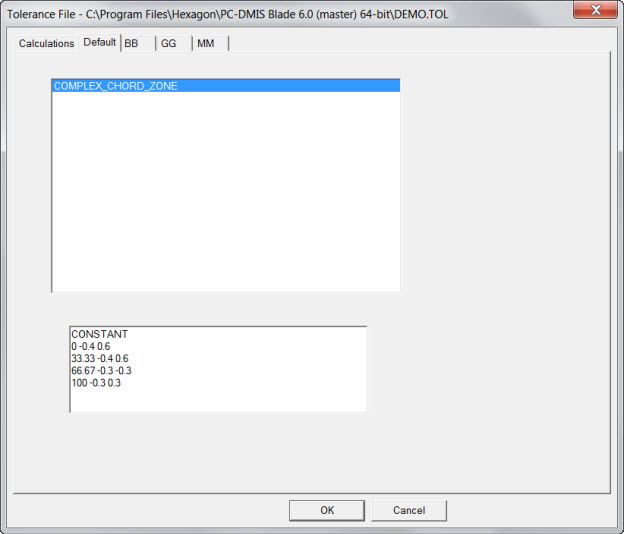
• 在默认选项卡上设置公差。当每个区域的参数相同时，可以使用此选项卡。在这种情况下，您无需为每个区域定义参数。

• 在单个截面选项卡上为每个单个截面自定义区域。如果在单个截面选项卡上选择区域，则可以在选项卡的框中输入参数。文本框中的格式如下所示：

复杂翼弦区的插值参数在指定的公差之间插入。这些参数为 SMOOTH、LINEAR 和 CONSTANT。其余的复杂翼弦区参数位于三列最多五十行的表中。该表必须具有两行或更多行。每行具有以下格式：

X <公差下限> <公差上限>

• 第一列X是距测尖的距离。如果第一距离为零，则表示该区域包括测尖；否则，该区域不包括测尖。值以任意单位表示，因为该区域始终从前缘测尖延伸到后缘测尖。它们可以是百分比、距离或任何彼此保持正确比例的单位。

• 第二列表示公差下限。公差下限值通常为负。

• 第三列是公差上限。公差上限值通常为正。

上下公差可以是对称的，但不是强制的。

对于SMOOTH和LINEAR参数，始终使用最后一行中的正公差和负公差，因为区域公差会插入到（线性或平滑地）最后一行的公差中。

对于CONSTANT参数，最后的正公差和负公差无关紧要。更具体地说，区域公差在每个距离间隔内都是恒定的。列出公差的行包含恒定区域大小开始的距离，恒定区域大小在下一行给出的距离处结束。这意味着最后一行中的正公差和负公差没有影响。它们可以是零，也可以是一个非常大的值，或者其他任何值。

以下是代表区域的COMPLEX_CHORD_ZONE参数的示例。它将叶片分为三个相等的部分：

(a) 部分为0％至33.33％，公差为-0.4至0.6。
(b) 部分为33.33%至66.67%，公差为-0.4至0.6。
(c) 部分为66.67%至100%，公差为-0.3至0.3。

COMPLEX_CHORD_ZONE示例

使用复杂的翼弦区

定义了复杂的翼弦区之后，就可以以算法文件中定义的最佳拟合使用它。复杂的翼弦区的最佳拟合算法为：

• 叶盆最小二乘方弦公差带

• 叶背最小二乘方弦公差带

• 叶盆最大最小值弦公差带

• 叶背最大最小值弦公差带

其中两个参数位于叶盆，另外两个位于叶背。另外，其中两个使用最小二乘法，另外两个则使用最小-最大法。所有这些拟合都可一次在整个区域上运行，并且始终适合于区域的中间。此外，这些拟合也适用于变量（不均匀）区域，这很重要，因为典型的翼弦区是可变（不均匀）的。

在算法文件中选择这些算法之一时，还必须为要使用的复杂区域选择复杂区域编号（1到10）。复杂区域的最佳拟合始终适合于公差带的中心，如果公差带是对称的，则它与标称曲线相同。如果公差带不对称，则公差带的中心与标称曲线不同。

复杂翼弦区最佳拟合也根据总公差的倒数来加权点。区域小的地方权重大。区域大的地方权重小。这意味着复杂的翼弦区绝对不应具有完全为零的总公差，因为那样会使权重无限大。

要使用复杂的翼弦区，请执行以下步骤：

1. 在算法文件中定义所需的最佳拟合算法。要定义它们，请决定要最小二乘还是最小最大，以及要叶盆还是叶背。

2. 使用CCCONT或CVCONT计算来定义所需的轮廓计算。使用DEVIATION_RATIO计算方法，因为翼弦区通常是可变的（不均匀）。DEVIATION_RATIO计算方法告诉您用于轮廓的区域部分。

• 介于0.0和1.0之间的值在公差内，因为它们表示轮廓适合该区域。

• 大于1.0的值超出公差范围，因为它们表示轮廓不适合该区域。

• 值越小越好；值越大越差。

3. 在“公差”文件中，将公差范围设置为[0.0，1.0]，以使一致性正确。每个公差都进入复杂的翼弦区。

轮廓图

您可以在轮廓图中绘制前缘最小二乘拟合。有关轮廓图的信息，请参见“创建轮廓图”。